The NumPy Python package

The NumPy website has some tutorials such as

NumPy: the absolute basics for beginners,
NumPy quickstart and
NumPy fundamentals
Tutorial: Linear algebra on n-dimensional arrays is a nice tutorial with an application to image compression.

Why NumPy?

Here's a fragment of code in the Python programming language.

result = 0
for i in range(100):
    result += i

Here is something similar in C.

int result = 0;
for(int i=0; i<100; i++){
    result += i;
}

In C the types of all variables are declared and fixed. In Python we can do this.

x = 4
x = "four"

But in C, we cannot. This gives an error.

int x = 4;
x = "four";

The standard Python interpreter is written in C. A Python int is a C structure something like this.

struct _longobject {
    long ob_refcnt;
    PyTypeObject *ob_type;
    size_t ob_size;
    long ob_digit[1];
};

where

ob_refcnt: is a counter of references to the structure
ob_type: encodes the type of the variable
ob_size: specifies the size of the following data members
ob_digit: contains the actual integer value

All of this information is required for Python to have the flexibility that it offers us. C only requires one long to store the integer.

We could use Python lists to represent arrays of numbers but that would be inefficient because Python lists are heterogeneous.

[23, 4.56, True, "Tuesday"]

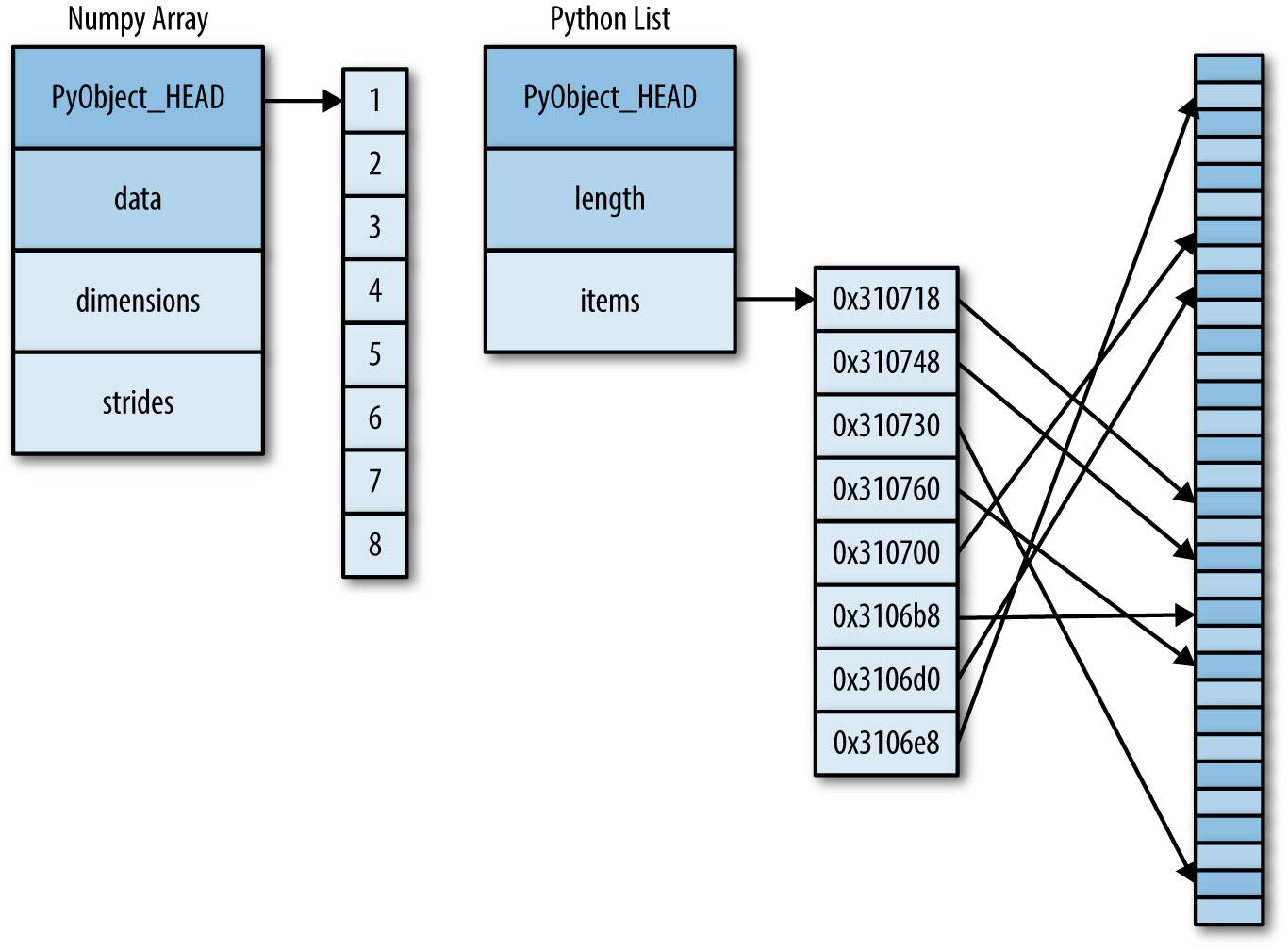
Figure 1: NumPy arrays vs Python lists

from numpy import arange
from time import perf_counter


class timeit:
    def __init__(self, text: str = None):
        self.text = text or "Time"

    def __enter__(self):
        self.start = perf_counter()
        return self

    def __exit__(self, type, value, traceback):
        self.time = perf_counter() - self.start
        self.readout = f"{self.text}: {self.time:.2e} seconds"
        print(self.readout)


size = 2**24

list1 = list(range(size))
list2 = list(range(size))

array1 = arange(size)
array2 = arange(size)

with timeit("Lists") as _t:
    resultantList = [(a * b) for a, b in zip(list1, list2)]

with timeit("Numpy") as _t:
    resultantArray = array1 * array2

Lists: 8.43e-01 seconds
Numpy: 2.47e-02 seconds

Data types

Data type	Description
`bool_`	Boolean (True or False) stored as a byte
`int_`	Default integer type (same as C long; normally either int64 or int32)
`intc`	Identical to C int (normally int32 or int64)
`intp`	Integer used for indexing (same as C ssize_t; normally either int32 or int64)
`int8`	Byte (–128 to 127)
`int16`	Integer (–32768 to 32767)
`int32`	Integer (–2147483648 to 2147483647)
`int64`	Integer (–9223372036854775808 to 9223372036854775807)
`uint8`	Unsigned integer (0 to 255)
`uint16`	Unsigned integer (0 to 65535)
`uint32`	Unsigned integer (0 to 4294967295)
`uint64`	Unsigned integer (0 to 18446744073709551615)
`float_`	Shorthand for float64
`float16`	Half-precision float: sign bit, 5 bits exponent, 10 bits mantissa
`float32`	Single-precision float: sign bit, 8 bits exponent, 23 bits mantissa
`float64`	Double-precision float: sign bit, 11 bits exponent, 52 bits mantissa
`complex_`	Shorthand for complex128
`complex64`	Complex number, represented by two 32-bit floats
`complex128`	Complex number, represented by two 64-bit floats

Creating

First we import numpy in the conventional way.

import numpy as np

`np.array([1,2,3])`	1d array
`np.array([(1,2,3),(4,5,6)])`	2d array
`np.arange(start,stop,step)`	range array
`np.linspace(0,2,9)`	Add evenly spaced values btw interval to array of length
`np.zeros((1,2))`	Create and array filled with zeros
`np.ones((1,2))`	Creates an array filled with ones
`np.random.random((5,5))`	Creates random array
`np.empty((2,2))`	Creates an empty array

When creating an array, NumPy will infer the type from the data given but you can specify it if you wish.

print([np.array([1, 2, 3], dtype="uint"), np.array([1.2, 3.4, 5.6], dtype="float")])

[array([1, 2, 3], dtype=uint64), array([1.2, 3.4, 5.6])]

Accessing array properties

`array.shape`	Dimensions (Rows,Columns)
`len(array)`	Length of Array
`array.ndim`	Number of Array Dimensions
`array.dtype`	Data Type
`array.astype(type)`	Converts to Data Type
`type(array)`	Type of Array

Indexing, slicing, selecting

`array[i]`	1d array at index i
`array[i,j]`	2d array at `index[i][j]`
`array[i<4]`	Boolean Indexing
`array[0:3]`	Select items of index 0, 1 and 2
`array[0:2,1]`	Select items of rows 0 and 1 at column 1
`array[:1]`	Select items of row 0 (equals `array[0:1, :]`)
`array[1:2, :]`	Select items of row 1
`array[ : :-1]`	Reverses array
`array > 5`	Array of Booleans
`array[array > 5]`	Boolean indexing

Copying, sorting

`np.copy(array)`	Creates copy of array
`other = array.copy()`	Creates deep copy of array
`array.sort()`	Sorts an array
`array.sort(axis=0)`	Sorts axis of array

Manipulation

Adding or Removing Elements

`np.append(a,b)`	Append items to array
`np.insert(array, 1, 2, axis)`	Insert items into array at axis 0 or 1
`np.resize((2,4))`	Resize array to shape(2,4)
`np.delete(array,1,axis)`	Deletes items from array

Combining

`np.concatenate((a,b),axis=0)`	Concatenates 2 arrays, adds to end
`np.vstack((a,b))`	Stack array row-wise
`np.hstack((a,b))`	Stack array column wise

Splitting

`np.split()`	Split an array into multiple sub-arrays.
`np.array_split(array, 3)`	Split an array in sub-arrays of (nearly) identical size
`np.hsplit(array, 3)`	Split the array horizontally at 3rd index

Linear algebra

`other = ndarray.flatten()`	Flattens a 2d array to 1d
`array = np.transpose(other)`	Transpose array
`array.T`
`inverse = np.linalg.inv(matrix)`	Inverse of a given matrix
`a @ b`	Matrix multiplication

Numerical calculations

Arithmetic and Trigonometry

`np.add(x,y)`
`x + y`	Addition
`np.substract(x,y)`
`x - y`	Subtraction
`np.divide(x,y)`
`x / y`	Division
`np.multiply(x,y)`
`x * y`	Multiplication
`np.matmul(x,y)`
`x @ y`	Matrix Multiplication
`np.sqrt(x)`	Square Root
`np.sin(x)`	Element-wise sine
`np.cos(x)`	Element-wise cosine
`np.log(x)`	Element-wise natural log
`np.dot(x,y)`	Dot product
`np.roots([1,0,-4])`	Roots of a given polynomial coefficients

Statistics

`np.mean(array)`	Mean
`np.std(array)`	Standard Deviation
`np.median(array)`	Median
`np.corrcoef(array)`	Correlation Coefficient
`array.sum()`	Array-wise sum
`array.min()`	Array-wise minimum value
`array.max(axis=0)`	Maximum value of specified axis
`array.cumsum(axis=0)`	Cumulative sum of specified axis

Slow loops, fast array computations

np.random.seed(0)


def compute_reciprocals(values):
    output = np.empty(len(values))
    for i in range(len(values)):
        output[i] = 1.0 / values[i]
    return output


values = np.random.randint(1, 10, size=5)
print(compute_reciprocals(values))

[0.16666667 1.         0.25       0.25       0.125     ]

big_array = np.random.randint(1, 100, size=1000000)

%timeit compute_reciprocals(big_array)

1.11 s ± 19.2 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

print(1.0 / values)

[0.16666667 1.         0.25       0.25       0.125     ]

%timeit (1.0 / big_array)

1.07 ms ± 8.68 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

The / operator here is a NumPy universal function or ufunc